文:「边缘琐事丶」 | 图:Pixabay
##前言
先问大家几个问题:
- 下午两点半有多少人在刷朋友圈?
- 北京有多少加油站?
- 芝加哥有多少调音师?
- 胡同口的煎饼摊子一年能卖多少个煎饼?

产品或市场方向的面试中,时不时会出现这些匪夷所思的问题,而面试官只给你几分钟的时间进行思考,让你做出合理的分析,并且给出答案。
作为一个产品小白,初次面对这样的问题真是无从下手。之后搜罗了不少文章,也留下了一些思考,写了点东西就迫不及待地想大家分享一下。
定义
这类问题被称为“费米问题”,英文名“Fermi Problem”,维基百科的词条是这么描述的:
In physics or engineering education, a Fermi problem, Fermi quiz, Fermi question, Fermi estimate, or order estimation is an estimation problem designed to teach dimensional analysis, approximation, and such a problem is usually a back-of-the-envelope calculation.
它往往被设计用于考察一个人多维度思考的逻辑思维能力,而回答它时,因为题述给出的已知条件几乎不存在,所以又可以看出一个人的知识面是否广泛,把它放在面试中可以说是再合适不过了。
这个问题真的有标准答案嘛?
估算问题,怎么可能有标准答案嘛!
这个问题答案显然是开放的,因为题述几乎不存在什么已知条件,所以我们并不需要去纠结给出的那个数字正确与否,而应该把更多的目光放在推理过程。
起源
在解决现在我们面试中碰到的费米问题之前,我们不妨先看看古人是怎么思考的。

众所周知,学术界存在的那些XX问题,基本上就是XX提出的。费米问题起源于**“费米悖论”**,那是1951年的一天……一个叫费米的人,仰望星空,问了一句:“外星人都在哪呢?”
银河系中有数十亿和太阳类似的恒星,其中很多比太阳系古老10亿年以上。其中一些恒星可能会有类似地球的行星,它们很可能也会孕育智慧生命。其中部分智慧生命可能会发展出星际飞行的科技。即使以我们现在能够想象的科技飞行,它们也能够在一百万年内飞遍整个星系。
但是,为什么我们在太空中没有看见一个智慧生命的影子呢?
一拍脑子想出来的问题,众说纷纭。一直到1961年,弗兰克·德雷克成名之作诞生——“宇宙文明方程式”。

其中:
$N$:银河系内可能与我们通讯的文明数量
$R^*$:银河系形成恒星的平均速率
$F_p$:恒星有行星的比例
$n_e$:每个行星系中类地行星数目
$f_l$:有生命进化可居住行星比例
$f_i$:演化出高智生物的概率
$f_c$:高智生命能够进行通讯的概率
$L$:科技文明寿命
通过参数相乘,我们便可以推算出银河系及可观测宇宙能与我们进行无线电通信的高智能文明数目。
看到这里,费米问题的思路就有了。
路径
我们可以将那些看似完全无法预测的问题拆解成一个个可以估算的小问题。就像N成为费米问题的答案,它不再代表的“外星人”的数量时,我们也应该把解决问题的思考聚焦在那一个个参数上面。
但我们怎么才能想到这些参数呢,是逻辑;这些参数如何取值呢,是知识储备。后者往往看个人积累,而前者我们却可以通过不断的训练而得出。
解答
笔者认为,常见费米问题的解答通常可以分为以下两类:
- 由点及面,由面及点的参数相乘
- 供需关系的参数相除
下面我们举例展开。
1.由点及面,由面及点的参数相乘
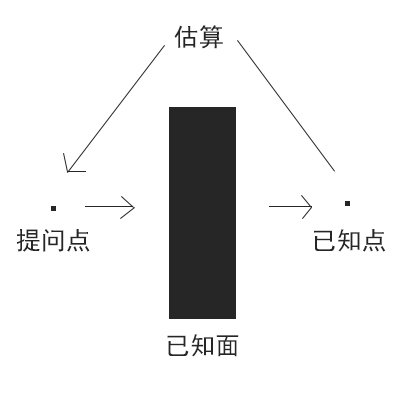
牛客网上有一个笔试题:如何预测周五下午两点半刷朋友圈的人数。
因为笔者还是在校学生,所以附加一个条件——学生党。
这个问题求的是一个很小的点,我们不妨先考虑一个面——整个用户群体,估测微信活跃用户量约为100,000万,出于计算简便和误差的综合考虑,我们将其分为两个用户群体:学生党、上班族,大致比例3:7吧,那么我们就可以得到微信活跃用户中学生党的数量。
再回到一个点,举一个典型的例子。从我自身出发,工作日的一天我一般会刷6次左右的朋友圈,其中3次会在饭后发生,下午一般是2次,自我判断我应该是属于朋友圈刷的比较少的那一类人,女生可能会更多,如6次。我们取平均数4次,每次时间一般为1分钟(假设一分钟后会刷到上次的内容),也就是在下午的四个小时240分钟内,估算学生党会有4分钟刷朋友圈的时间。那么在2:30(假设下午的时间每个点都一样)的概率就是1/60。
所以,周五下午两点半刷朋友圈的人数(学生党)
= 微信用户量100,000万 × 学生党比例3/10 × 下午2:30刷朋友圈的概率1/60
=500万
2.供需关系的参数相除

大部分的问题,都可以从供需关系展开。
有些是真实的供需问题,比如北京加油站问题:
- 需求:北京机动车数量*每辆机动车多久加一次油,按天计算,即每天北京的机动车要加A次油
- 供应:每个加油站每天可以给B辆车加油
再比如芝加哥钢琴师问题:
-
需求:芝加哥每年有A架钢琴需要调
-
供应:一位钢琴师一年可以调B架钢琴
需求和供应都是一个个参数堆叠出来的小问题,解决了A和B,最后的答案两者相除就可以得到,即N=A/B。
有些供需问题很简单,甚至不需要考虑需求,比如煎饼摊问题,煎饼是属于现做现卖的产品,所以几乎是没有库存的,也就是做多少卖多少。
这样的问题,我们只需要考虑供应就行了。在一个大佬的回答中,他取早上一个时段饱和状态下卖出的数量,能卖出360个煎饼作为上限;若赚取的毛利润刚好维持生计,则每天至少卖出67个,作为下限。取几何平均,再乘上一年的天数,得出56.7K这个数字。
其实题目做多了,会发现很多问题都是供需问题,只是供需很抽象罢了。
总结
在回答完问题后,还有个比较重要的事情——误差分析,我们应该去指出自己的估算中,有哪些采样是容易产生较大的误差的,产生误差的因素是什么。这样做可以体现思考问题的全面,也许会成为面试中一个很大的加分点。
懂了那么些“套路”后,发现回答费米问题还是一件很有意思的事情。碰到一眼看不出来的问题,就换个角度,或许就产出了一个思路清奇的答案。
所以孙悟空到底有几个女朋友呀~